Notes: Are we still writing spaghetti code?

Note1.

Wikipedia defines spaghetti code as source code that has a complex and tangled control structure, especially one using many GOTO statements, exceptions, threads, or other "unstructured" branching constructs. These statements clearly reside within methods, yet this post discusses spaghetti code on class- and package-level. Is this justifiable?

Well, another name for that, "Control structure," is control flow, the order in which individual statements, instructions or function calls of an imperative program are executed or evaluated. So two criteria must be fulfilled to be able to evaluate something as spaghetti code: it must have statements and these statements must obey control flow.

Classes are mere containers of statements, and just as statements obey ordered execution, so too can the parts of classes in which they reside be considered to obey ordered execution. Dependencies between classes represent precisely this ordering: a dependency between class A and B such that A B implies that some part of A is executed before some part of B. Thus control flow exists at class-level, justifying an evaluation of this class-level control as potential spaghetti code.

The same argument also holds for packages, which are also mere containers of statements.

Note2.

Difficulties abound. Let's go back a step, and consider figure 7. Say someone updates this figure so that b() also calls f(), see figure 8.

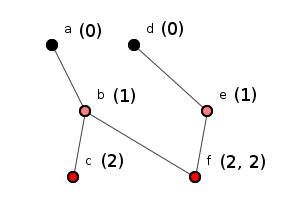
Figure 8: A terrifying complication.

Now we see that f() has two depth values. Why? Because when we list our transitive dependencies we see we now have three and f() is in two of them.

a(0) b(1) c(2)
a(0) b(1) f(2, 2)
d(0) e(1) f(2, 2)

To check for total ordering, we need to check a method's depth value, and when it comes to f() we must chose between two number, though in this case they are both equal. But what if f() were deeper in the transitive dependency d(0) e(1) x(2) f(2, 3), as in figure 9? Which would we chose then?

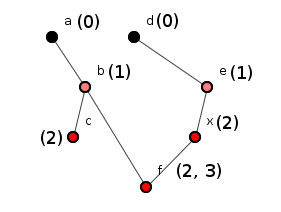
Figure 9: Two uneven transitive dependencies.

Here, we make the supposition mentioned earlier: we assert that a method's depth is the minimum of its positions in all its transitive dependencies.

In this instance, even with this supposition, the system enjoys total ordering, as the depths values never fall in any of its transitive dependencies - not even in: d(0) e(1) x(2) f(2)

In fact, we'll go even further. We want to err on the side of over-sensitivity, so we will judge each pair of nodes in a dependency by selecting the maximum depth of the calling node in all its transitive dependencies and the minimum depth of the called node. This is how Spoiklin Soice calculates structure disorder.

Note3.

Here's that table again, averaged over levels for each program.

Program	Method	Class	Package	Average
Cassandra	41	82	84	69
Zookeeper	28	85	93	69
ActiveMQ Broker	24	80	89	64
Jenkins	26	72	90	63
JUnit	34	78	76	63
Camel	22	90	70	61
Lucene	33	70	73	59
FitNesse	33	55	61	50
Tomcat (Coyote)	22	81	40	48
Maven	30	30	74	45
Log4j	25	59	47	44
Struts	11	42	74	42
Spring	27	60	35	41
Netty	22	69	20	37
Spoiklin Soice	26	25	3	18
Average	27	65	62	52

Table 3: The structural disorder of 15 Java programs, averaged over levels.

Note4.

We omit jar-level as jar files don't appear as first class entities in Java source code. There is nothing inherently wrong, however, in considering jars a fourth layer of structure and modules a fifth. No analysis on jar-level structure with respect to disorder has yet been performed.