Encapsulation theory: the minimised, uniformly violational radial branch.
Edmund Kirwan*
www.EdmundKirwan.com
Abstract
This paper investigates how the hidden elements of a single radial branch should be distributed so as to minimise the branch's potential coupling.
Keywords
Encapsulation theory, radial encapsulation, branch, potential coupling.
1. Introduction
In the absolute encapsulation context when an encapsulated set is uniformly-distributed in violational elements, then its potential coupling is minimised when it is also uniformly-distributed in hidden elements (see proposition 1.11 in [1]). In the radial encapsulation context, however, this is not the case. This paper demonstrates this phenomenon using an example branch and derives the equation showing the hidden element distribution that achieves a minimum potential coupling.
This paper considers sets of radial information-hiding only.
2. Selected branch potential couplings
Consider the branch shown in figure 1, showing a branch of three disjoint primary sets, where the information-hiding and the information-hiding violation of the sets are shown within their representative symbols.
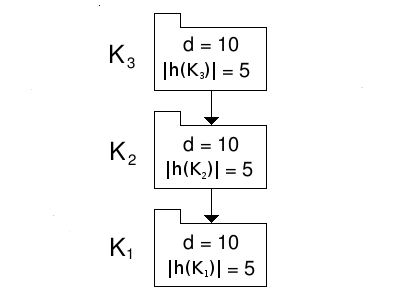
Figure 1: A branch of three disjoint primary sets.
Thus,
taking the root set, K1, for example, we see
that K1 has 10 violational elements,![]() =10,
and 5 hidden elements,
=10,
and 5 hidden elements,![]() =5;
as we are concerned here with uniform violational distributions, we
will discuss the specific violation of each set, and use the variable
that we normally use for specific violations, hence d=10,
though the meaning of both is, of course, the same. We note that
violational and hidden elements of the branch are distributed
uniformly throughout the sets.
=5;
as we are concerned here with uniform violational distributions, we
will discuss the specific violation of each set, and use the variable
that we normally use for specific violations, hence d=10,
though the meaning of both is, of course, the same. We note that
violational and hidden elements of the branch are distributed
uniformly throughout the sets.
Let us calculate the potential coupling of this branch.
The potential coupling of K3 is the sum of its internal and external potential couplings. The internal potential coupling of K3 is the total number of contained elements multiplied by this number minus one, i.e., 15x14=210. The external potential coupling of K3 is the total number of contained elements multiplied by the total number of violational elements it can see "below" it, i.e., 15x(10+10)=300. So the potential coupling of K3 is 210+300=510.
As K2 has the same number of contained elements then it will have the same internal potential coupling as K3, i.e., 210. K2 can only see 10 violational elements "below" it, so its external potential coupling is 15x10=150. So the potential coupling of K2 is 210+150=360.
K1 has the same internal potential coupling as the other two, i.e., 210, and K1 has, like all root sets, no external potential coupling (there are no sets "below" it for it to see), so its potential coupling is the same as its internal potential coupling, 210.
The branch's potential coupling is then: 510+360+210=1080.
We know that, in the absolute encapsulation context, potential coupling is minimised (ignoring A.M.C.s) when both the violational and hidden element are distributed uniformly over all sets. Let us test to see whether this also holds in the radial encapsulation context: let us move a hidden element from K2 to K1, see figure 2.
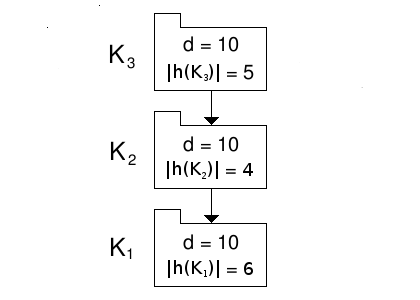
Figure 2: A branch of three disjoint primary sets.
Now let us calculate the potential coupling of this modified branch.
The potential coupling of K3 is unchanged.
The potential coupling of K2 has now fallen from 360 to 14x13+14x10=322.
The potential coupling of K1 has now risen from 210 to 16x15 = 240.
The branch's total potential coupling has now fallen from 1080 to 510+322+240=1072.
Thus by moving a hidden element, thereby rendering the branch non-uniformly distributed in hidden elements, we have reduced the branch's potential coupling. We note that the branch is still uniformly distributed in violational elements. This then raises the obvious question: given a branch that is uniformly distributed in violational elements, what distribution of hidden elements will minimise its potential coupling?
This question is of practical relevance as we suspect that a branch's minimum potential coupling will be achieved when each set in the branch has the minimum number of violational elements, and that minimum is one. In putting one element in each set, however, we are automatically uniformly distributing the violational elements, hence the configuration of a branch at its minimum potential coupling is one in which it is uniformly distributed in violational elements.
It can be shown that, to attain the minimum potential coupling in this case, the number of hidden elements in the ith disjoint primary set is given by the following equation (see proposition 9.12):
![]()
With this equation we can calculate the number of hidden elements in each of the three sets examined above to minimise the potential coupling.
K3 should contain the following number of hidden elements:
![]()
K2 should contain the following number of hidden elements:
![]()
K1 should contain the following number of hidden elements:
![]()
The branch thus configured is shown in figure 3.
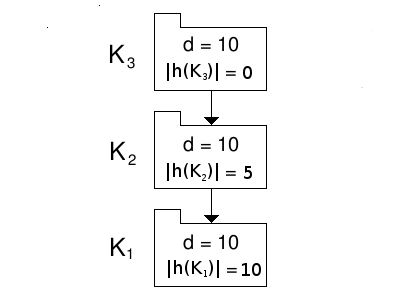
Figure 3: A branch non-uniformly distributed in hidden elements with minimised potential coupling.
Calculating the potential coupling of this minimised branch we see the following.
The potential coupling of K3 is 10x9+10x20=290.
The potential coupling of K2 is 15x14+15x10=360.
The potential coupling of K1 is 20x19 = 380.
The branch's total potential coupling is 290+360+380=1030, down from the original, uniformly distributed figure of 1080.
3. Observations
The reduction of potential coupling achievable using the equation above to guide hidden element distribution is a function of the specific violation, d, the number of violational elements per disjoint primary set. In a well-encapsulated set, d is small, therefore the reduction of potential coupling achievable using this distribution will not be great in well-encapsulated sets of sets.
It is noteworthy, however, that this hidden element distribution favours packing the hidden elements towards the lower end of the branch. In software development, for example, this argues against, "Top heavy," branches and recommends that leaf subsystems and leaf packages should not contain an above average number of program units.
4. Conclusion
When a branch is uniformly distributed in violational elements, its minimum potential coupling is not achieved by also uniformly distributing its hidden elements. Instead, an equation describes the hidden element distribution to achieve this minimum potential coupling and this equation suggests placing more hidden elements towards the lower part of the branch than the higher.
5. Appendix A
5.1 Propositions
Proposition 9.1
Given
a branch B in encapsulated set G of n elements
and of r disjoint primary sets, with each disjoint primary set
having an information-hiding violation of d, the internal
potential coupling of the ith primary set,![]() ,
is given by:
,
is given by:
![]()
Proof:
By definition [D1.2] in [1],
given a primary set Qi the internal
potential coupling![]() is
given by:
is
given by:
![]() (i)
(i)
By definitions [D1.2], [D1.6] and [D1.7] of [1], the elements in Ki are those in the intersection of Ki with H and V, or:
![]() (ii)
(ii)
By definition [D1.1] in [1], H and V are disjoint so taking the cardinality of (ii) gives:
![]() (iii)
(iii)
By definition, each disjoint primary set has an information-hiding violation of d, so substituting into (iii) gives:
![]() (iv)
(iv)
Substituting (iv) into (i) gives:
![]()
=![]()
QED
Proposition 9.2
Given
a branch B in encapsulated set G of n elements
and of r disjoint primary sets, with each disjoint primary set
having an information-hiding violation of d, the external
potential coupling of the ith primary set,![]() ,
is given by:
,
is given by:
![]()
Proof:
By proposition 8.11 in [3],
given a primary set Qi of a single branch
the external potential coupling is![]() given
by:
given
by:
![]() (i)
(i)
By definitions [D1.2], [D1.6] and [D1.7] of [1], the elements in Ki are those in the intersection of Ki with H and V, or:
![]() (ii)
(ii)
By definition [D1.1] in [1], H and V are disjoint so taking the cardinality of (ii) gives:
![]() (iii)
(iii)
By definition, each disjoint primary set has an information-hiding violation of d, so substituting into (iii) gives:
![]() (iv)
(iv)
Substituting (iv) into (i) gives:
![]()
=![]()
QED
Proposition 9.3
Given
a branch B in encapsulated set G of n elements
and of r disjoint primary sets, with each disjoint primary set
having an information-hiding violation of d, the potential
coupling of the ith primary set,![]() ,
is given by:
,
is given by:
![]()
Proof:
By proposition 9.1, the internal
potential coupling of the ith primary set,![]() ,
is given by:
,
is given by:
![]() (i)
(i)
By proposition 9.2, the external
potential coupling of the ith primary set,![]() ,
is given by:
,
is given by:
![]() (ii)
(ii)
By proposition 8.7 in [3], the potential coupling of Qi is the sum of the external potential coupling sets of Qi and the internal potential coupling of Qi, or:
![]() (iii)
(iii)
Substituting (i) and (ii) into (iii) gives:
![]()
QED
Proposition 9.4
Given
a branch B in encapsulated set G of n elements
and of r disjoint primary sets, with each disjoint primary set
having an information-hiding violation of d, the potential
coupling of B,![]() ,
is given by:
,
is given by:
![]()
Proof:
By definition I SHOULD PROVE THIS ????????????????????????xxx, the potential coupling of a branch is the sum of the potential couplings of all its sets, or:
![]() (i)
(i)
By proposition 9.3, the
potential coupling of the ith primary set,![]() ,
is given by:
,
is given by:
![]() (ii)
(ii)
Substituting (ii) into (i) gives:
![]()
=![]()
QED
Proposition 9.5
Given
a branch B in encapsulated set G of n elements
and of r disjoint primary sets, with each disjoint primary set
having an information-hiding violation of d, the potential
coupling of B,![]() ,
is given by:
,
is given by:
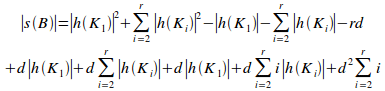
Proof:
By proposition 9.4, the
potential coupling of B,![]() ,
is given by:
,
is given by:
![]() (i)
(i)
By definition:
![]() (ii)
(ii)
Applying (ii) to (i) gives:
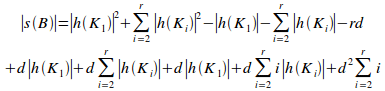
=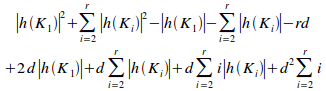
QED
Proposition 9.6
Given a branch B in encapsulated set G of n elements and of r disjoint primary sets, with each disjoint primary set having an information-hiding violation of d, the number of elements in B is given by:
![]()
Proof:
By definition, the number of elements in a branch is the sum of the number of elements in all its disjoint primary sets, or:
![]() (i)
(i)
By definitions [D1.2], [D1.6] and [D1.7] of [1], the elements in Ki are those in the intersection of Ki with H and V, or:
![]() (ii)
(ii)
By definition [D1.1] in [1], H and V are disjoint so taking the cardinality of (ii) gives:
![]() (iii)
(iii)
By definition, each disjoint primary set has an information-hiding violation of d, so substituting into (iii) gives:
![]() (iv)
(iv)
Substituting (iv) into (i) gives:
![]()
=![]()
=![]()
QED
Proposition 9.7
Given
a branch B in encapsulated set G of n elements
and of r disjoint primary sets, with each disjoint primary set
having an information-hiding violation of d, the number of
information-hidden elements in the first primary set,![]() ,
is given by:
,
is given by:
![]()
Proof:
By proposition 9.6 the number of elements in B is given by:
![]()
=![]()
![]()
QED
Proposition 9.8
Given
a branch B in encapsulated set G of n elements
and of r disjoint primary sets, with each disjoint primary set
having an information-hiding violation of d, the square of the
number of information-hidden elements in the first primary set,![]() ,
is given by:
,
is given by:
![]()
Proof:
By proposition 9.7 the number of
information-hidden elements in the first primary set,![]() ,
is given by:
,
is given by:
![]() (i)
(i)
Squaring both sides of (i) gives:
![]()
QED
Proposition 9.9
Given
a branch B in encapsulated set G of n elements
and of r disjoint primary sets, with each disjoint primary set
having an information-hiding violation of d, the potential
coupling of B,![]() ,
is given by:
,
is given by:
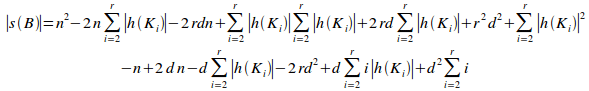
Proof:
By proposition 9.5 the potential
coupling of B,![]() ,
is given by:
,
is given by:
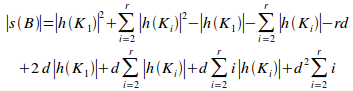 (i)
(i)
By proposition 9.7 the number of
information-hidden elements in the first primary set,![]() ,
is given by:
,
is given by:
![]() (ii)
(ii)
By proposition 9.8 the square of
the number of information-hidden elements in the first primary set,![]() ,
is given by:
,
is given by:
![]() (iii)
(iii)
Substituting (ii) and (iii) into (i) gives:
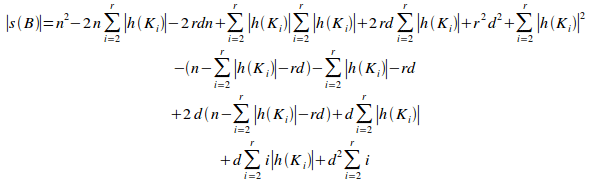
=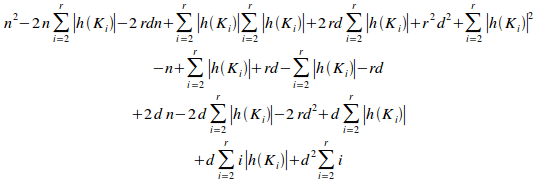
=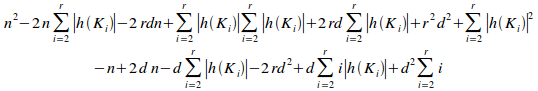
QED
Proposition 9.10
Given
a branch B in encapsulated set G of n elements
and of r disjoint primary sets, with each disjoint primary set
having an information-hiding violation of d, the number of
information-hidden elements in the ith
primary set,![]() ,
where
,
where![]() ,
which minimises the potential coupling of B is given by:
,
which minimises the potential coupling of B is given by:
![]()
Proof:
By proposition 9.9, the
potential coupling of B,![]() ,
is given by:
,
is given by:
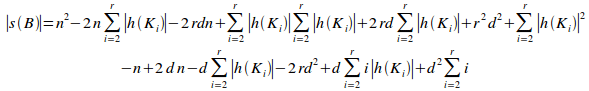 (i)
(i)
To find the value of![]() which
minimises this potential coupling we must differentiate (i)
w.r.t.
which
minimises this potential coupling we must differentiate (i)
w.r.t.![]() and
set to zero:
and
set to zero:
![]()
![]() (ii)
(ii)
By proposition 9.7, the number
of information-hidden elements in the first primary set,![]() ,
is given by:
,
is given by:
![]()
![]() (iii)
(iii)
Substituting (iii) into (ii) gives:
![]()
=![]()
![]()
QED
Proposition 9.11
Given
a branch B in encapsulated set G of n elements
and of r disjoint primary sets, with each disjoint primary set
having an information-hiding violation of d, the number of
information-hidden elements in the first primary set,![]() which
minimises the potential coupling of B is given by:
which
minimises the potential coupling of B is given by:
![]()
Proof:
By proposition 9.7, the number
of information-hidden elements in the first primary set,![]() ,
is given by:
,
is given by:
![]() (i)
(i)
By proposition 9.10, the number
of information-hidden elements in the ith
primary set,![]() ,
where
,
where![]() ,
which minimises the potential coupling of B is given by:
,
which minimises the potential coupling of B is given by:
![]() (ii)
(ii)
Substituting (ii) into (i) gives:
![]()
=![]()
=![]()
=![]()
=![]()
=![]()
![]()
![]()
=![]()
=![]()
QED
Proposition 9.12
Given
a branch B in encapsulated set G of n elements
and of r disjoint primary sets, with each disjoint primary set
having an information-hiding violation of d, the number of
information-hidden elements in the ith
primary set,![]() which
minimises the potential coupling of B is given by:
which
minimises the potential coupling of B is given by:
![]()
Proof:
By proposition 9.10, the number
of information-hidden elements in the ith
primary set,![]() ,
where
,
where![]() ,
which minimises the potential coupling of B is given by:
,
which minimises the potential coupling of B is given by:
![]() (i)
(i)
By proposition 9.11, the number
of information-hidden elements in the first primary set,![]() which
minimises the potential coupling of B is given by:
which
minimises the potential coupling of B is given by:
![]() (ii)
(ii)
Substituting (ii) into (i) gives:
![]()
=![]()
=![]()
QED
6. References
[1] - "Encapsulation theory fundamentals," Ed Kirwan, www.EdmundKirwan.com/pub/paper1.pdf
[2] - "Encapsulation theory: the minimised, uniformly violational radial branch," Ed Kirwan, www.EdmundKirwan.com/pub/paper9.pdf
[3] - "Encapsulation theory: radial encapsulation," Ed Kirwan, www.EdmundKirwan.com/pub/paper8.pdf
*© Edmund Kirwan 2009. Revision 1.0, December 20th 2009. (Revision 1.0: December 20th, 2009.) All entities may republish, but not for profit, all or part of this material provided reference is made to the author and title of this paper. The latest revision of this paper is available at [2].













